Dynamical Systems and Differential Equations

Lec 27 | MIT 18.03 Differential Equations, Spring 2006

Order: Reorder
Duration: 50:25
Updated: 08 Aug 2013

Sketching Solutions of 2x2 Homogeneous Linear System with Constant Coefficients View the complete course: http://ocw.mit.edu/18-03S06 License: Creative Commo...

http://wn.com/Lec_27_|_MIT_1803_Differential_Equations,_Spring_2006

Linearizing non-linear dynamic equations

Order: Reorder
Duration: 7:27
Updated: 17 Jul 2013

In this lecture, we go through the steps of linearizing non-linear differential equations about a given operating/equilibrium point. We will use the multi-va...

http://wn.com/Linearizing_non-linear_dynamic_equations

Multiagent Dynamical Systems

Order: Reorder
Duration: 56:46
Updated: 20 Jul 2013

I will show how to model multiagent systems using dynamical systems theory by deriving a class of macroscopic differential equations that describe mutual ada...

http://wn.com/Multiagent_Dynamical_Systems

Differential Equations - Solve Linear System using Laplace transforms

Order: Reorder
Duration: 14:48
Updated: 22 Jul 2013

Solve the system: dx/dt + 3x + dy/dt = 1, dx/dt - x + dy/dt - y = e^t, x(0)=0, y(0)=0

http://wn.com/Differential_Equations_Solve_Linear_System_using_Laplace_transforms

Rotational Dynamic System Modeling Example

Order: Reorder
Duration: 6:40
Updated: 10 Jan 2014

This is a quick review of how to generate differential equations for a system having rotating disks, torsional stiffness and torsional damping.

http://wn.com/Rotational_Dynamic_System_Modeling_Example

State Space Representation ( Dynamic Systems ) | Mechanical Engineering

Order: Reorder
Duration: 9:01
Updated: 04 Aug 2013

State Space Representation Dynamic Systems.

http://wn.com/State_Space_Representation_Dynamic_Systems_|_Mechanical_Engineering

Taxonomy of Dynamic Systems

Order: Reorder
Duration: 9:40
Updated: 03 Jul 2013

An overview of the ways to classify dynamic systems (differential equations) based on continuity, linearity and time variance.

http://wn.com/Taxonomy_of_Dynamic_Systems

Simulink tutorial: Second Order Dynamic System

Order: Reorder
Duration: 5:52
Updated: 05 Jun 2013

This tutorial shows how to create a 2nd order system in Simulink. The code can be found in the tutorial section in http://www.eeprogrammer.com/. More enginee...

http://wn.com/Simulink_tutorial_Second_Order_Dynamic_System

Solving Differential Equations by LT part 2

Order: Reorder
Duration: 14:00
Updated: 07 Oct 2013

http://wn.com/Solving_Differential_Equations_by_LT_part_2

Differential Equations: The Exponential Map Perspective - Lecture 1

Order: Reorder
Duration: 48:25
Updated: 06 Sep 2013

The first in a series of lectures which will examine differential equations from the perspective of the exponential map. The first lecture starts by considering real exponents, where several key exponent properties are assumed to be true for ALL REAL NUMBERS (this was not made clear in the lecture). From there, we derive several basic exponent properties that we know from basic algebra. We begin to study Taylor series, and will eventually define complex exponents using the exponential function. This will serve as a spring-board towards demonstrating the importance of the exponential function in mathematics, and the ideas will be used later on when we talk about the exponential of a matrix. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold. This lecture occurred on Sept. 5th, 2013.

http://wn.com/Differential_Equations_The_Exponential_Map_Perspective_Lecture_1

Mythily Ramaswamy - Control of Differential Equations

Order: Reorder
Duration: 39:44
Updated: 08 Oct 2013

PROGRAM: RECENT TRENDS IN ERGODIC THEORY AND DYNAMICAL SYSTEMS DATES: Tuesday 18 Dec, 2012 - Saturday 29 Dec, 2012 VENUE: Department of Mathematics,Faculty of Science, The Maharaja Sayajirao University of Baroda, Vadodara PROGRAM LINK: http://www.icts.res.in/program/ETDS2012 DESCRIPTION: "Dynamical Systems" is an exciting and very active field in mathematics that involves tools and techniques from many areas. A dynamical system can be obtained by iterating a function or letting evolve in time the solution of an equation. Even if the rule of evolution is deterministic, the long term behavior of the system is often chaotic. Different branches of "Dynamical Systems", in particular "Ergodic Theory", provide tools to quantify this chaotic behavior of the system and to predict it in an average. This program has been planned in two parts: 7 day Workshop (Dec 18-24, 2012) followed by 4 day Discussion Meeting (Dec 26-29, 2012). The aim is to bring together on one platform experts from around the world who are actively working in various sub-disciplines of Dynamical Systems. An important aspect of the program will be an emphasis on making it accessible to younger participants. The workshop will begin with lectures on basic Ergodic Theory followed by lectures on Topological Dynamics, Differentiable Dynamics and Symbolic Dynamics, including Cellular Automata. It will have a `problem and discussion' session every day. Many researchers from across the globe will be discussing their celebrated works in Ergodic Theory, Dynamical Systems and related areas during the four days of the Discussion Meeting. We will encourage young participants to present a short communication on their work in the presence of the eminent experts during the program.

http://wn.com/Mythily_Ramaswamy_Control_of_Differential_Equations

Differential Equations, The Exponential Map Perspective - Lecture 10

Order: Reorder
Duration: 28:36
Updated: 22 Nov 2013

The tenth in a series of lectures which will examine differential equations from the perspective of the exponential map. The tenth lecture discusses coordinates, and change of basis. We introduce the basic features of the Jordan Normal Form. The Jordan Normal Form puts a matrix into a form which is extremely easy to exponentiate. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold. The tenth lecture was recorded on November 21st, 2013.

http://wn.com/Differential_Equations,_The_Exponential_Map_Perspective_Lecture_10

Differential Equations, The Exponential Map Perspective - Lecture 7

Order: Reorder
Duration: 40:08
Updated: 25 Oct 2013

The seventh in a series of lectures which will examine differential equations from the perspective of the exponential map. The seventh lecture continues with very basic concepts from linear algebra. We are moving towards the Jordan Normal Form. The Jordan Normal Form puts a matrix into a form which is extremely easy to exponentiate. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold.

http://wn.com/Differential_Equations,_The_Exponential_Map_Perspective_Lecture_7

Lecture 3

Order: Reorder
Duration: 53:18
Updated: 21 Sep 2013

The third in a series of lectures which will examine differential equations from the perspective of the exponential map. The third lecture develops the complex logarithm. This will serve as a spring-board towards demonstrating the importance of the exponential function in mathematics, and the ideas will be used later on when we talk about the exponential of a matrix. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold. This lecture occurred on Sept. 19th, 2013.

http://wn.com/Lecture_3

Differential Equations: The Exponential Map Perspective - Lecture 9

Order: Reorder
Duration: 37:29
Updated: 16 Nov 2013

The ninth in a series of lectures which will examine differential equations from the perspective of the exponential map. The ninth lecture discusses coordinates, and change of basis. We are moving towards the Jordan Normal Form. The Jordan Normal Form puts a matrix into a form which is extremely easy to exponentiate. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold.

http://wn.com/Differential_Equations_The_Exponential_Map_Perspective_Lecture_9

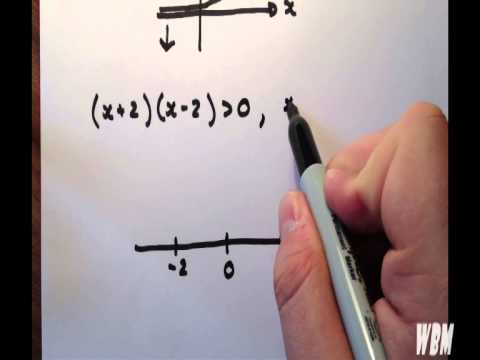
How To: Find the Domain of a Function #2

Order: Reorder
Duration: 4:09
Updated: 13 Jan 2014

I hope you found this video useful, please subscribe for daily videos! WBM Foundations: Mathematical logic Set theory Algebra: Number theory Group theory Lie groups Commutative rings Associative ring theory Nonassociative ring theory Field theory General algebraic systems Algebraic geometry Linear algebra Category theory K-theory Combinatorics and Discrete Mathematics Ordered sets Geometry Geometry Convex and discrete geometry Differential geometry General topology Algebraic topology Manifolds Analysis Calculus and Real Analysis: Real functions Measure theory and integration Special functions Finite differences and functional equations Sequences and series Complex analysis Complex variables Potential theory Multiple complex variables Differential and integral equations Ordinary differential equations Partial differential equations Dynamical systems Integral equations Calculus of variations and optimization Global analysis, analysis on manifolds Functional analysis Functional analysis Fourier analysis Abstract harmonic analysis Integral transforms Operator theory Numerical analysis and optimization Numerical analysis Approximations and expansions Operations research Probability and statistics Probability theory Statistics Computer Science Computer science Information and communication Applied mathematics Mechanics of particles and systems Mechanics of solids Fluid mechanics Optics, electromagnetic theory Classical thermodynamics, heat transfer Quantum Theory Statistical mechanics, structure of matter Relativity and gravitational theory Astronomy and astrophysics Geophysics applications Systems theory Other sciences Category

http://wn.com/How_To_Find_the_Domain_of_a_Function_2

Modeling and control of dynamic systems - From electric vehicles to systems biology : Adachi's Group

Order: Reorder
Duration: 3:55
Updated: 15 Apr 2013

At the Adachi Laboratory, the theme of research is modeling and control. Control means actively changing a systems dynamics in a desired way. Control is util...

http://wn.com/Modeling_and_control_of_dynamic_systems_From_electric_vehicles_to_systems_biology_Adachi's_Group

Differential Equations, The Exponential Map Perspective - Lecture 8

Order: Reorder
Duration: 26:06
Updated: 09 Nov 2013

The eighth in a series of lectures which will examine differential equations from the perspective of the exponential map. The eighth lecture discusses eigenvalues and eigenvectors. We are moving towards the Jordan Normal Form. The Jordan Normal Form puts a matrix into a form which is extremely easy to exponentiate. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold.

http://wn.com/Differential_Equations,_The_Exponential_Map_Perspective_Lecture_8

Solving Differential Equations by LT part 1

Order: Reorder
Duration: 10:01
Updated: 07 Oct 2013

http://wn.com/Solving_Differential_Equations_by_LT_part_1

System Dynamics and Control: Module 3 - Mathematical Modeling Part I

Order: Reorder
Duration: 65:34
Updated: 18 Aug 2013

Discussion of differential equations as a representation of dynamic systems. Introduction to the Laplace Transform as a tool for solving differential equations.

http://wn.com/System_Dynamics_and_Control_Module_3_Mathematical_Modeling_Part_I

Differential Equations: The Exponential Map Perspective - Lecture 6

Order: Reorder
Duration: 38:20
Updated: 18 Oct 2013

The sixth in a series of lectures which will examine differential equations from the perspective of the exponential map. The sixth lecture introduces very basic concepts from linear algebra. We are moving towards the Jordan Normal Form. The Jordan Normal Form puts a matrix into a form which is extremely easy to exponentiate. Differential equations, matrix theory, dynamical systems, exponential map, exponents, complex numbers, Taylor series, taylor polynomials, sequences, series, vector field, equilibrium, linearization, stable manifold, unstable manifold. This lecture occurred on Sept. 19th, 2013.

http://wn.com/Differential_Equations_The_Exponential_Map_Perspective_Lecture_6

How To: Find the Domain of a Function #3

Order: Reorder
Duration: 4:04
Updated: 13 Jan 2014

I hope you found this video useful, please subscribe for daily videos! WBM Foundations: Mathematical logic Set theory Algebra: Number theory Group theory Lie groups Commutative rings Associative ring theory Nonassociative ring theory Field theory General algebraic systems Algebraic geometry Linear algebra Category theory K-theory Combinatorics and Discrete Mathematics Ordered sets Geometry Geometry Convex and discrete geometry Differential geometry General topology Algebraic topology Manifolds Analysis Calculus and Real Analysis: Real functions Measure theory and integration Special functions Finite differences and functional equations Sequences and series Complex analysis Complex variables Potential theory Multiple complex variables Differential and integral equations Ordinary differential equations Partial differential equations Dynamical systems Integral equations Calculus of variations and optimization Global analysis, analysis on manifolds Functional analysis Functional analysis Fourier analysis Abstract harmonic analysis Integral transforms Operator theory Numerical analysis and optimization Numerical analysis Approximations and expansions Operations research Probability and statistics Probability theory Statistics Computer Science Computer science Information and communication Applied mathematics Mechanics of particles and systems Mechanics of solids Fluid mechanics Optics, electromagnetic theory Classical thermodynamics, heat transfer Quantum Theory Statistical mechanics, structure of matter Relativity and gravitational theory Astronomy and astrophysics Geophysics applications Systems theory Other sciences Category

http://wn.com/How_To_Find_the_Domain_of_a_Function_3

Logical Analysis of Hybrid Systems

Order: Reorder
Duration: 53:31
Updated: 30 Jul 2013

RI Seminar, February 18, 2011 Andre Platzer Assistant Professor, Computer Science Department, Carnegie Mellon University Hybrid systems model cyber-physical ...

http://wn.com/Logical_Analysis_of_Hybrid_Systems